Exemplos práticos:
Qual seria a data Tzolkin/Haab que corresponderia ao 1 de janeiro de 1995 do calendário civil gregoriano?
Em primeiro lugar, devemos achar a data juliana, como dissecado em Conhecimentos Gerais... 2) Não confundir calendário juliano com período juliano
Suprimindo-se agora os 13 dias (período gregoriano) conforme tabela, teremos : 2.449.718,75 ou, arredondando, 2.449.719 dias (dias julianos).
Em segundo lugar, deveremos calcular quantos dias decorreram desde o marco ZERO do calendário maia até 1 de janeiro de 1995; isso é elementar, senão vejamos:
Posteriormente, divide-se o número 1.865.436 por 260 e 365 (calendários Tzolkin e Haab), obtendo-se respectivamente as frações:
Finalmente, recorremos ao calendário Tzolkin Permanente (página anterior) e ao calendário Haab Permanente, correlacionando as frações, enquadramos a data maia como sendo:
No que diz respeito à Contagem Longa (Long Cont) para o mesmo primeiro de janeiro de 1995 tivemos: (zero hora)
Basicamente, a finalidade desse ciclo, cujo nome não se conhece, era conciliar o ano Haab de 365 dias como o ano Tzolkin de 260.
A conciliação entre os sistemas dava-se de 52 em 52 anos, como poderemos acompanhar nas demonstrações abaixo:
Ciclo do ano solar = 4 anos
Ciclo do ano religioso = 13 meses
O mínimo múltiplo comum de 4 e 13 é = 52
52 anos X 365 dias= 18.980 dias
73 X 260 dias = 18.980 dias
Não havia numeração seqüencial do ano solar. Em virtude do ciclo de 52 anos, que os maias denominavam de A Volta do Calendário, dificilmente um cidadão vivia mais do que duas voltas do mesmo (104 anos).
O mais extraordinário no sistema era que ao fundirem os dois calendários (religioso e solar), uma data somente se repetiria após 18.980 dias.
Os dois sistemas, Tzolkin e Haab, iniciavam ao mesmo tempo e, somente decorridos 18.980 dias, 73 anos religiosos e 52 anos solares, os dois primeiros dias dos respectivos calendários emparelhavam-se.
Qual seria a data Tzolkin/Haab que corresponderia ao 1 de janeiro de 1995 do calendário civil gregoriano?
Em primeiro lugar, devemos achar a data juliana, como dissecado em Conhecimentos Gerais... 2) Não confundir calendário juliano com período juliano
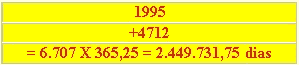
Suprimindo-se agora os 13 dias (período gregoriano) conforme tabela, teremos : 2.449.718,75 ou, arredondando, 2.449.719 dias (dias julianos).
Em segundo lugar, deveremos calcular quantos dias decorreram desde o marco ZERO do calendário maia até 1 de janeiro de 1995; isso é elementar, senão vejamos:

Posteriormente, divide-se o número 1.865.436 por 260 e 365 (calendários Tzolkin e Haab), obtendo-se respectivamente as frações:

Finalmente, recorremos ao calendário Tzolkin Permanente (página anterior) e ao calendário Haab Permanente, correlacionando as frações, enquadramos a data maia como sendo:

No que diz respeito à Contagem Longa (Long Cont) para o mesmo primeiro de janeiro de 1995 tivemos: (zero hora)


Basicamente, a finalidade desse ciclo, cujo nome não se conhece, era conciliar o ano Haab de 365 dias como o ano Tzolkin de 260.
A conciliação entre os sistemas dava-se de 52 em 52 anos, como poderemos acompanhar nas demonstrações abaixo:
Ciclo do ano solar = 4 anos
Ciclo do ano religioso = 13 meses
O mínimo múltiplo comum de 4 e 13 é = 52
52 anos X 365 dias= 18.980 dias
73 X 260 dias = 18.980 dias
Não havia numeração seqüencial do ano solar. Em virtude do ciclo de 52 anos, que os maias denominavam de A Volta do Calendário, dificilmente um cidadão vivia mais do que duas voltas do mesmo (104 anos).
O mais extraordinário no sistema era que ao fundirem os dois calendários (religioso e solar), uma data somente se repetiria após 18.980 dias.
Os dois sistemas, Tzolkin e Haab, iniciavam ao mesmo tempo e, somente decorridos 18.980 dias, 73 anos religiosos e 52 anos solares, os dois primeiros dias dos respectivos calendários emparelhavam-se.




0 Comments:
Postar um comentário
<< Home